Neem een test met 10 meerkeuzevragen, met vier alternatieven bij elke vraag. Bij een goed antwoord krijg je drie punten, voor een blanco nul punten en voor een fout antwoord gaat er een punt af. Veronderstel dat je van vier vragen het antwoord weet, dan moet je op een aantal van de overige vragen gokken om toch kans te maken om te slagen. Wat is dan je beste strategie?
Het maximum aantal punten dat kan toegekend worden is 30 en slagen betekent dus minstens 15 punten scoren. We noteren met b het aantal vragen dat je blanco laat, met g = 10 – 4 – b = 6 – b het aantal vragen waarop je gokt en met f het aantal vragen dat je fout gegokt hebt. je eindscore bedraagt dan:
![]()
We berekenen naargelang het aantal vragen dat je gokt de kans op slagen:
- Veronderstel g = 1, dan is b = 5 en je eindscore is 15 – 4f en dit moet minstens 15 zijn. Hieruit volgt dat f nul moet zijn. Je slaagkans is dus de kans op geen fout antwoord als je 1 keer gokt en dat is
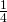 of 25%.
of 25%. - Veronderstel g = 2, dan is b = 4 en je voor je eindscore geldt
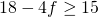 . Ook hier moet dus f = 0. De slaagkans is de kans op 0 fouten bij twee keer gokken en dat is
. Ook hier moet dus f = 0. De slaagkans is de kans op 0 fouten bij twee keer gokken en dat is 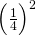 en dat is 6,25%.
en dat is 6,25%. - Veronderstel g = 3, dan is b = 3 en je voor je eindscore geldt
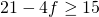 . Hieruit volgt dat f = 0 of f = 1. De slaagkans is
. Hieruit volgt dat f = 0 of f = 1. De slaagkans is 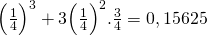 of 15,625%. Dit kan ook berekend worden via Binomcdf(3,
of 15,625%. Dit kan ook berekend worden via Binomcdf(3,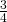 ,1).
,1). - Veronderstel g = 4, dan is b = 2 en je voor je eindscore geldt
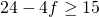 . Hieruit volgt dat f = 0 , f = 1 of f = 2. De slaagkans bedraagt Binomcdf(4,
. Hieruit volgt dat f = 0 , f = 1 of f = 2. De slaagkans bedraagt Binomcdf(4,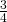 ,2) =0,26171875 of 26,17%.
,2) =0,26171875 of 26,17%. - Veronderstel g = 5, dan is b = 1 en je voor je eindscore geldt
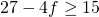 . Hieruit volgt dat f = 0 , f = 1 ,f = 2 of f = 3. De slaagkans bedraagt Binomcdf(5,
. Hieruit volgt dat f = 0 , f = 1 ,f = 2 of f = 3. De slaagkans bedraagt Binomcdf(5,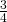 ,3) =0,3671875of 36,72%.
,3) =0,3671875of 36,72%. - Veronderstel g = 6, dan is b = 0 en je voor je eindscore geldt
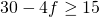 . Hieruit volgt dat f = 0 , f = 1 ,f = 2 of f = 3. De slaagkans bedraagt Binomcdf(6,
. Hieruit volgt dat f = 0 , f = 1 ,f = 2 of f = 3. De slaagkans bedraagt Binomcdf(6, ,3) =0,16943 of 16,94%.
,3) =0,16943 of 16,94%.
De beste strategie is één vraag blanco te laten en 5 keer te gokken. Dan heb je 36,72% kans om te slagen.