Tag archieven: euclides

Griekse wiskunde deel 6

Geplaatst op door

Over de mens Euclides is weinig bekend, We weten dat hij rond 300 v.C. wiskunde doceerde in het museion van Alexandrië. Gevormd in de scholen van Plato en Aristoteles, is hij dus één van de Griekse intellectuelen die naar Alexandrië toestroomden om er beroepsgeleerde te worden. 

Uit de analyse van zijn werken is vrij duidelijk te zien dat Euclides geen groot wiskundige was, maar wel een buitengewone didacticus. Zo ligt het geniale van zijn Elementen niet zozeer in de inhoud, want die is afkomstig van zijn grote voorgangers Archytas, Theatetus en Eudoxos. Maar het bijzondere is de gepaste keuze van de volgorde, waar de verschillende onderdelen worden behandeld. Een vrij omvangrijk eerste deel is ook toegankelijk voor middelmatige leerlingen, de moeilijke delen komen pas later aan de beurt.

De elementen staat zeker op de lijst van de boeken die het grootst aantal uitgaven en vertalingen hebben gekend. Deze bestseller omvat 13 boeken, waaraan door latere wiskundigen nog 2 boeken zijn toegevoegd. ( o.a. een boek over regelmatige veelvlakken). De boeken 1 tot 4 handelen over de meetkunde van de rechte, de driehoek en de cirkel. Boeken 5 en 6 zijn gewijd aan de leer van de evenredigheden en de gelijkvormige figuren. In boeken 7,8 en 9 gaat het over de natuurlijke getallen. Boek 10 bestudeert de irrationale getallen. Tenslotte gaat het in de boeken 11,12 en 13 over de meetkunde van de ruimte en de 5 regelmatige veelvlakken.

Euclidische getallen

Geplaatst op door

Een Euclidisch getal van de eerste soort is een getal van de vorm E_n=p_1.p_2.\cdots.p_n+1, waarbij p_1,...,p_n de eerste n priemgetallen voorstellen. De getallen danken hun naam aan de Griekse wiskundige Euclides, die ze gebruikte in zijn bewijs dat er oneindig veel priemgetallen zijn. Stel dat er maar een eindig aantal priemgetallen zou zijn , zeg n. Noteer die dan door p_1,p_2,...,p_n. Neem dan het getal x=p_1.p_2.....p_n+1. Het getal x geeft bij deling door alle priemgetallen p_i als rest 1. Bijgevolg is x zelf ook een priemgetal, dat groter is dan alle gegeven priemgetallen. Dit is onmogelijk, dus moeten er oneindig veel priemgetallen zijn.

Zo is E_1=2+1=3, E_2=2.3+1=7, E_3=2.3.5+1=31. Dan komen 211,2311, 30031,…

  • Niet alle Euclidische getallen zijn priem. Het eerste niet-priemgetal is   2.3.5.7.11.13 = 30031 = 59 × 509 . Een open vraag is of er oneindig veel Euclidische getallen zijn die priem zijn.
  • Elk Euclidisch getal laat bij deling door 4 een rest gelijk aan 4 na. Dit komt omdat 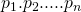p_1.p_2.....p_n, juist 1 factor 2 bevat.
  • Bijgevolg kan een Euclidisch getal nooit een kwadraat zijn.
  • Voor 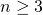n \geq 3 is het cijfer der eenheden van 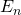E_n altijd een 1.

Een Euclidisch getal van de tweede soort is een getal van de vorm E_n=p_1.p_2.\cdots.p_n-1, waarbij p_1,...,p_n de eerste n priemgetallen voorstellen. De eerste euclidische getallen van de tweede soort zijn  1, 5, 29, 209, 2309, 30029, 510509, 9699689,… Ook hier weten we eigenlijk niet of er oneindig veel Euclidische getallen zijn die priem zijn. In ieder geval het eerste niet priemgetal in de rij is 209 = 11 x 19.

Niet-Euclidische meetkunde

Geplaatst op door

 

De meetkunde, die we dagelijks gebruiken, wordt Euclidische meetkunde genoemd, ter ere van Euclides, die tussen 330 en 320 voor Christus een aantal boeken, genaamd „Elementen” geschreven heeft.

Hierin wordt  de meetkunde opgebouwd met stellingen vertrekkend van een vijftal postulaten of axioma’s: 
1. Door 2 verschillende punten gaat juist 1 rechte.
2. Een lijnstuk kan naar beide kanten onbeperkt worden
    verlengd.
3. Er kan met elk middelpunt en elke straal een cirkel
    getrokken worden.
4. Alle rechte hoeken zijn gelijk.
5. Door een punt P buiten een rechte , gaat precies één rechte
    die evenwijdig loopt met  de eerste rechte.

Dit laatste axioma staat bekend als het parallellenpostulaat.
Eeuwen heeft men gedacht dat men dit postulaat kon bewijzen aan de hand van de andere vier axioma’s. Trouwens de formulering van het parallellenpostulaat was oorspronkelijk anders.  De gegeven formulering komt van John Playfair. Deze formulering stamt uit 1795 en staat bekend als “Playfair’s axioma” . Een andere gelijkwaardige formulering van dit postulaat is dat de hoekensom van een driehoek gelijk is aan 180°.

Het duurde tot de 19 de eeuw voor het juist inzicht er kwam en wel bij 3 wiskundigen ongeveer gelijktijdig en waarschijnlijk onafhankelijk van elkaar: C.F.Gauss, J.Bolyai en I.Lobatschefsky.

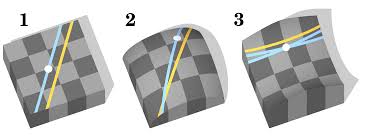
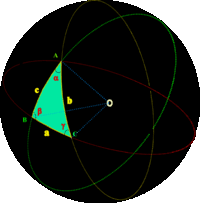
Het was Joha,, Bolyai die tot het inzicht kwam dat het mogelijk was een meetkunde op te stellen, waarin door een punt buiten een rechte oneindig veel rechten gaan die de gegeven rechte niet snijden. Hij publiceerde zijn ideeën in 1832 en gaf zo gestalte aan de hyperbolische meetkunde. De som van de hoeken van een driehoek is hier minder dan 180°.  In de hyperbolische meetkunde wordt dus niet meer aan het parallellenpostulaat voldaan.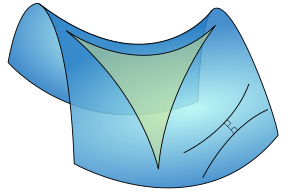 
Later werd ook de elliptische meetkunde ontdekt. Elliptische meetkunde is een niet-Euclidische meetkunde, waarbij door een punt buiten een rechte  geen andere rechten bestaat die de gegeven rechte niet snijdt.

De gewone meetkunde is dus niet de meetkunde, maar een  meetkunde. Met andere axioma’s krijgen we een ander soort meetkunde.

Afstanden

Geplaatst op door

We kennen allemaal het visueel evidente begrip afstand  als ” de lengte van het deel van de rechte lijn tussen twee punten”, dat  ontleend is aan de klassieke meetkunde. Daarbij bleef de term “rechte lijn” zelf ongedefinieerd of hoogstens werd er gezegd dat het de kortste weg was tussen twee punten, waarmee men in een cirkelredenering terecht kwam.

Bovendien is de afstand langs de rechte lijn niet altijd geschikt voor het oplossen van veel praktische en theoretische problemen.

  1. Een transportfirma is bij het opstellen van een vervoersplan niets gebaat met de kennis van de afstanden in vogelvlucht tussen vertrek en aankomst, daar de vrachtwagens verplicht zijn het bestaande verkeersnet te volgen.
  2. Een schip of vliegtuig is tijdens zijn reis verplicht de kromming van de aarde te volgen, daar het nu eenmaal niet mogelijk is in een rechte lijn door de aardkorst te boren.
  3. Hoe zou je bijvoorbeeld de afstand tussen twee functies ( nodig bij het bestuderen van de convergentie van een rij van functies)  kunnen definiëren?

In de wiskunde is een begrip afstand of metriek gedefinieerd als generalisatie van het gewone afstandsbegrip. Deze generalisatie is zo gekozen dat een aantal kenmerkende eigenschappen van het gewone afstandsbegrip behouden blijven.

Een afstand of metriek in een verzameling V is een afbeelding d  die met twee elementen uit  V een getal laat associëren die de volgende eigenschappen bezit:

  1. De afstand is positief: d(x,y) \geq 0.
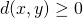  2. x ligt even ver van y als y van x ( symmetrie ): d(x,y)=d(y,x).
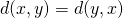  3. Een omweg maken is steeds langer dan de rechtstreekse weg te nemen
    ( driehoeksongelijkheid ):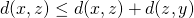 d(x,z) \leq d(x,z)+d(z,y)
  4. Iedere x ligt op een afstand 0 van zichzelf: d(x,x)=0
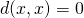
  5. Het omgekeerde van vorige eigenschap: d(x,y)=0 \leftrightarrow x=y

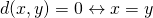
Een paar voorbeelden in het vlak:

  • De Euclidische afstand of metriek, gegeven door 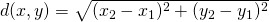d(x,y)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} komt overeen met ons klassiek begrip afstand.
  • De Manhattan metriek,voor het eerst onderzocht aan het eind van de 19e eeuw door Hermann Minkowski, en wordt gegeven door 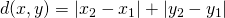d(x,y)=|x_2-x_1|+|y_2-y_1|  De naam verwijst naar de roostervormige opzet van de meeste lanen en straten op het eiland Manhattan, zoals vastgelegd in een plan uit 1811. Dit rooster zorgt ervoor dat de kortste route die een voetganger of auto kan nemen om de afstand tussen twee punten in de stad te overbruggen een lengte heeft die gelijk is aan de afstand tussen twee punten in de Manhattan-metriek. In onderstaande tekening zijn de lijnen in rood, geel en blauw  drie voorbeelden van de Manhattan-afstand tussen de twee zwarte, ronde punten. Zij zijn alle drie 12 eenheden lang. De groene lijn stelt de volgens de Euclidische afstand kortste route voor tussen de twee punten.
    Een ander voorbeeld kan je ook vinden in de codetheorie , waar men de Hamming-afstand definieert door het aantal posities te tellen waar de twee binaire codes van elkaar verschillen