Een eutrigon is een willekeurige driehoek waarvan 1 hoek 60 graden meet. De zijde ertegenover noemt men de hypotenusa van het eurtrigon.
Men kan op de zijden van een eutrigon gelijkzijdige driehoeken construeren, zoals in onderstaande tekening: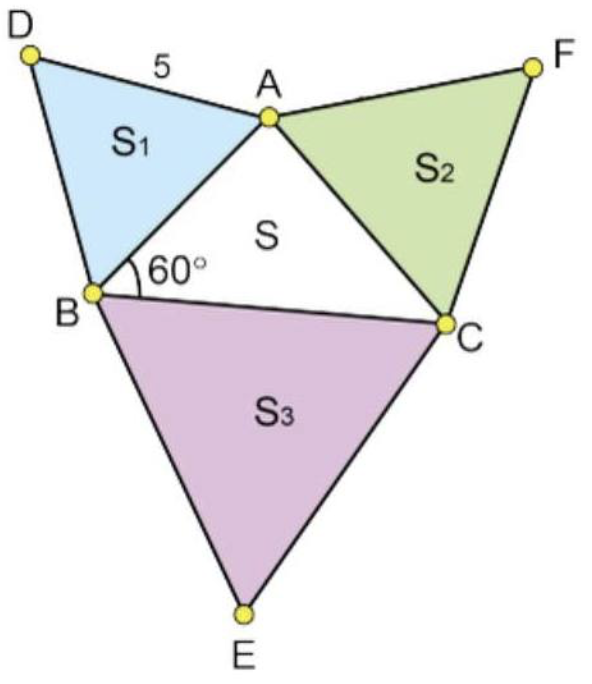
Er bestaat een stelling die zegt dat de som van de oppervlakten van de eutrigon en de driehoek op de hypotenusa, gelijk is aan de som van de oppervlakte van de driehoeken op de twee andere zijden:
![Rendered by QuickLaTeX.com \[S+S_2=S_1+S_3\]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-5d6b5873b35feda520e2d1383714e2c0_l3.png)
In driehoek ABC kan je de cosinusregel toepassen:
![Rendered by QuickLaTeX.com \[b^2=a^2+c^2-ac\]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-49992605234b608eb8914608cf9d05cc_l3.png)
De oppervlakte van een gelijkzijdige driehoek met zijde z wordt gegeven door de formule:
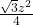
. Verder weten we dat de oppervlakte van driehoek ABC gegeven wordt door
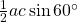
. Als we beide leden in de cosinusregel van hierboven vermenigvuldigen met
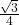
, vinden we dat
![Rendered by QuickLaTeX.com \[S+S_2=S_1+S_3\]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-5d6b5873b35feda520e2d1383714e2c0_l3.png)
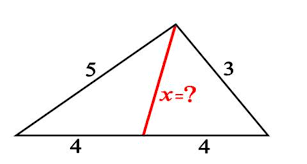
![]() van de zwaartelijn uit A berekenen in functie van de zijden a, b en c van de driehoek?
van de zwaartelijn uit A berekenen in functie van de zijden a, b en c van de driehoek?![]() te berekenen en de bekomen resultaten optelt vind je:
te berekenen en de bekomen resultaten optelt vind je: ![]()
![]()