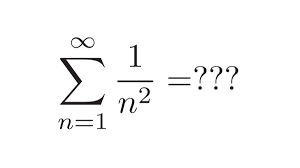Tag archieven: euler

Lhuilier

Geplaatst op door

De studie van veelvlakken kan teruggevoerd worden naar de piramiden van het Oude Egypte. Maar het waren voornamelijk de Grieken die geïnteresseerd waren in de wiskundige eigenschappen van regelmatige veelvlakken. Zij ontdekten  de 5 platonische lichamen, waarvan een volledige beschrijving werd gegeven door Theiatetos ( 400 BC).

In 1750 formuleerde Euler(1707-1783) een formule die een verband legt tussen het aantal zijvlakken, het aantal hoekpunten  en het aantal ribben van een veelvlak: Z – R + H = 2. We zeggen dat deze veelvlakken Eulerkarakteristiek 2 hebben.

Maar Euler zag één punt over het hoofd, namelijk de kwestie van convexiteit. De veelvlakken die Euler en de Grieken bestudeerden, waren allemaal convex zonder dat dit expliciet werd verondersteld. In 1619 beschreef Kepler een regelmatig niet-convex veelvlak, namelijk de stella octangula. 

De kwestie van de convexiteit heeft dan ook geleid tot uitzonderingen op de formule van Euler. In 1811 vond Lhuilier( 1750-1840), een Zwitserse wiskundige, 3 soorten veelvlakken waarvoor de formule niet meer klopte. Deze soorten veelvlakken waren echter convex. 

Het was uiteindelijk Poincaré die de formule van Euler veralgemeende tot : Z – R + H = 2 – 2g, waar bij g het aantal gaten in het veelvlak is.

Het probleem van Bazel

Geplaatst op door

Het probleem van Bazel is een beroemd probleem uit de staltheorie. Het werd voor het eerst in 1644 aan de orde gesteld door Pietro Mengoli (1626-1686), en werd bijna 100 jaar later, in 1735, opgelost door Euler.

Het probleem vraagt:

Deze reeks is bij benadering gelijk aan 1,644934.  Euler slaagde erin de exacte uitkomst te geven: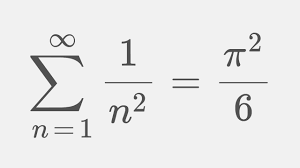

Het probleem heeft geleid tot nieuwe inzichten in de structuur van de reële getallen en de complexe getallen, en heeft bijgedragen tot de ontwikkeling van de analytische getaltheorie.

De Riemann-zeta functie \zeta is een belangrijke functie in de wiskunde vanwege het verband met de verdeling van de priemgetallen. De bovenstaande reeks is niets minder dan \zeta(2). Het omgekeerde getal  \frac{6}{\pi^2} is de kans dat twee willekeurige gehele getallen onderling ondeelbaar zijn.

Paardenrondgang

Geplaatst op door

Een paardenrondgang is een route bestaande uit paardensprongen op een schaakbord zodat elk veld van het schaakbord juist 1 keer wordt aangedaan.

De oude Arabieren konden dit al: Al-Adli, uit een manuscript uit het jaar 840

Een andere vastgelegde paardenrondgang is een oplossing  uit 1733 van de Franse wiskundige Lemoivre.  Speciaal was de oplossing van Euler . Hij
presenteert een opgevuld schaakbord met een rondgang waarvan de op volgorde genummerde sprongen op het bord ook een (half)magisch vierkant voorstellen met de magische som 260 (de som op de diagonalen klopt niet)

Deze rondgang was niet gesloten, met andere woorden eind en beginpunt vallen niet samen. Dat dit wel kon , liet in 1849 een Hongaar, Wenzelides zien: 

 

Er zijn wel  honderdzes biljoen verschillende gesloten paardronden. In augustus 2003 werd bekend dat de Fransman Meyrignac een 156 jaar oud wiskundig probleem had opgelost; dat van de ‘volledig magische paardronde’. Een door hem afgerichte supercomputer kwam er na 61 dagen rekenen achter dat die paardronde niet bestaat.

 

Een korte geschiedenis van pi

Geplaatst op door

Pi is de verhouding tussen de omtrek en de middellijn van een cirkel:

    \[\pi=\dfrac{\text{omtrek}}{\text{middellijn}}\]

Dit leidt tot de misvatting dat pi een rationaal getal is, want het kan geschreven worden als een breuk! We vergeten hierbij dat, in een breuk, felle en noemer gehele getallen moeten zijn. Maar bij pi is hetzij de omtrek , hetzij de diameter irrationaal. 

Het idee van pi als constante bestaat al lang. De Egyptenaren schatten het op \frac{25}{8}=3,125 en de Mesopotamiërs gaven het de waarde van \sqrt{10}\approx 3,162.

Archimedes was de eerste die pi grondig onderzocht. Door veelhoeken in een cirkel te  tekenen en hun omtrek te berekenen, kon hij pi schatten tussen \frac{223}{71} en \frac{22}{7}. sinds Archimedes is de nauwkeurigheid van pi groter geworden. Dank zij de computer kennen we nu pi tot op miljarden cijfers nauwkeurig.

Een paar schattingen door de eeuwen heen:

  • papyrus Rhind ( 1650 BC) :  3,16045
  • Archimedes (250 BC) : 3,1418
  • Ptolemaeus (150 AD) 3,14166
  • Brahmagupta (640 AD): 3,1622   
  • Al-Khwarizmi (800 AD) : 3,1416
  • Fibonacci (1220 AD) : 3,141818

Het symbool \pi, voor pi werd in 1706 geïntroduceerd door William Jones in zijn boek Synopsis Palmariorum Mathesis. 

Pi kan ook voorgesteld worden door een reeks . De veertiende eeuws Indiase wiskundige Madhava gebruikte de volgende reeks :

    \[\frac{\pi}{4}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}\cdots\]

Dit convergeert eerder traag naar pi. Euler gebruikte de reeks :

    \[\frac{\pi^2}{6}=1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\frac{1}{5^2}\cdots\]

De Engelse wiskunde Wallis maakte gebruik van:

    \[\frac{\pi}{2}=\frac{2}{1}*\frac{2}{3}*\frac{4}{3}*\frac{4}{5}*\frac{6}{5}\cdots\]

 

Het getal e

Geplaatst op door

Het product 1.2.3.4….n wordt genoteerd door n! en noemt men n faculteit. De grootte van de faculteiten neemt zeer snel toe:
1!=1
2!=2
3!=6
4!=24
5!=120
6!=720
7!=5040
8!=40320
9!=362880
10!=3628800

Even snel nemen dus de waarden van de termen in de volgende som af:

    \[a_n=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\frac{1}{4!}+\cdots +\frac{1}{n!}\]

We kunnen verwachten dat, naarmate n groter wordt, de waarde van a_n zeer weinig zal toenemen en een bepaald getal niet zal overschrijden. We kunnen aantonen dat a_n kleiner blijft dan 3.

Als we in k! elke factor, behalve de eerste, vervangen door 2, dan zien we duidelijk dat  k!> 2^{k-1}. Bijgevolg is a_n kleiner dan 1+1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\cdots+\frac{1}{2^{n-1}}. Vanaf de tweede term herken je hierin de som van de termen van een meetkundige rij.De limiet hiervan is \frac{1}{1-0,5}=2. Hieruit volgt dat , voor toenemende n waarden, a_n zeker kleiner is dan 1+2=3.

De getallen a_n zijn termen van een naar boven begrensde , stijgende rij en dus zal die rij convergeren. Die limiet noemen we het getal e. Met a_{12} te berekenen vindt we dat e\approx 2,7182818.

 


Het was de Schotse wiskundige John Napier die het eerst met dit getal geconfronteerd werd, toen hij werkte aan de eerste rekenlinialen.

Het getal werd door Euler het exponentiële getal genoemd. Vandaar ook, waarschijnlijk, de letter e voor dit getal. Het was ook Euler die de meeste eigenschappen van dit getal vond.