Tag archieven: pi

22/7

Geplaatst op door

Vroeger vertelde men ons dat we voor \pi de breuk \frac{22}{7} mochten nemen. Natuurlijk drong het niet bij iedereen door dat dit een benadering was. Een bewijsje:

Neem de functie

    \[f(x)=\frac{x^4(1-x)^4}{1+x^2}\]

  • f is strikt positief en continu tussen 0 en 1.
  • Dus is \int_0^1f(x) dx>0.
  • De Euclidische deling geeft \frac{x^4(1-x)^4}{1+x^2}=x^6-4x^5+5x^4-4x^2+4-\frac{4}{1+x^2}.
  • Een primitieve functie van f is dan \frac{1}{7}x^7-\frac{4}{6}x^6-x^5-\frac{4}{3}x^3+4x-4\text{Bgtan }(x).
  • Bijgevolg is \int_0^1f(x) dx= \frac{22}{7}-\pi. 
  • Uit het tweede puntje volgt dan:
  • Narekenen op rekentoestel geeft \frac{22}{7}=3,142857142857,... en \pi=3,14159265....

Een korte geschiedenis van pi

Geplaatst op door

Pi is de verhouding tussen de omtrek en de middellijn van een cirkel:

    \[\pi=\dfrac{\text{omtrek}}{\text{middellijn}}\]

Dit leidt tot de misvatting dat pi een rationaal getal is, want het kan geschreven worden als een breuk! We vergeten hierbij dat, in een breuk, felle en noemer gehele getallen moeten zijn. Maar bij pi is hetzij de omtrek , hetzij de diameter irrationaal. 

Het idee van pi als constante bestaat al lang. De Egyptenaren schatten het op \frac{25}{8}=3,125 en de Mesopotamiërs gaven het de waarde van \sqrt{10}\approx 3,162.

Archimedes was de eerste die pi grondig onderzocht. Door veelhoeken in een cirkel te  tekenen en hun omtrek te berekenen, kon hij pi schatten tussen \frac{223}{71} en \frac{22}{7}. sinds Archimedes is de nauwkeurigheid van pi groter geworden. Dank zij de computer kennen we nu pi tot op miljarden cijfers nauwkeurig.

Een paar schattingen door de eeuwen heen:

  • papyrus Rhind ( 1650 BC) :  3,16045
  • Archimedes (250 BC) : 3,1418
  • Ptolemaeus (150 AD) 3,14166
  • Brahmagupta (640 AD): 3,1622   
  • Al-Khwarizmi (800 AD) : 3,1416
  • Fibonacci (1220 AD) : 3,141818

Het symbool \pi, voor pi werd in 1706 geïntroduceerd door William Jones in zijn boek Synopsis Palmariorum Mathesis. 

Pi kan ook voorgesteld worden door een reeks . De veertiende eeuws Indiase wiskundige Madhava gebruikte de volgende reeks :

    \[\frac{\pi}{4}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}\cdots\]

Dit convergeert eerder traag naar pi. Euler gebruikte de reeks :

    \[\frac{\pi^2}{6}=1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\frac{1}{5^2}\cdots\]

De Engelse wiskunde Wallis maakte gebruik van:

    \[\frac{\pi}{2}=\frac{2}{1}*\frac{2}{3}*\frac{4}{3}*\frac{4}{5}*\frac{6}{5}\cdots\]

 

Nootje 8

Geplaatst op door

Stel de aarde voor als een gladde bol en span om die gladde aarde een touw  over de evenaar. De lengte van dat touw is ongeveer 40.000 km.
Maar stel je nu eens voor, dat we dat touw zouden doorknippen en er één meter tussen zouden knopen. We zouden het dan overal kunnen optillen tot het weer een cirkel zou vormen concentrisch met de evenaar.  Zou er dan een vlieg onder door kunnen?

Antwoord

  • De lengte van het touw is de omtrek van de cirkel en die wordt gegeven door O=2\pi R, met R de aardstraal.
  • Noteer x, de lengte waarmee de straal toeneemt als je de omtrek met 1 meter zou vermeerderen. Dan geldt

        \[2\pi(R+x)=2\pi R+1\]

  • Het uitwerken van deze vergelijking geeft

        \[x=\frac{1}{2\pi}\approx 0,16 m\]

  • Dus ongeveer 16 cm. Daar kan dus zeker een vlieg onder!
  • De uitkomst is onafhankelijk van de straal van de aarde. Je kan dus om het even welke cirkel gebruiken.

Oppervlakte van een cirkel

Geplaatst op door

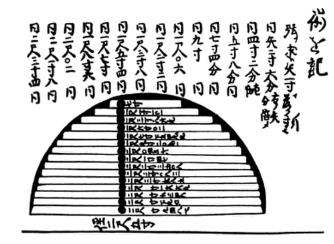
Het berekenen van de oppervlakte van een cirkel is een moeilijke zaak. Door de jaren heen heeft men geprobeerd een steeds betere benadering te vinden. Uiteraard valt dit probleem samen met het benaderen van pi. Bovenstaande tekening laat zien hoe ze dit probleem aanpakten in het zeventiende eeuwse Japan.

In het boek Kaison-ki Kömoku (1687 na Chr.), geschreven door Mochinaga Toyotsugu en Öhashi Takusei zien we dat ze de oppervlakte van een halve cirkel probeerden te benaderen door daarin smalle rechthoeken te tekenen en de oppervlakten daarvan op te tellen. Een beetje zoals de Riemann sommen… Het was de tijd waarin de sangaku’s werden gemaakt en Japan helemaal van de westerse wereld was afgezonderd.

Als we hun resultaat bekijken vinden we dat ze voor pi de waarde 3,01262848 bekwamen.

 

Madhava of Sangamagrama

Geplaatst op door

Madhava ( c.1340 – c. 1425) was een Indische wiskundige en astronoom die een formule vond voor \frac{\pi}{4}.

Toch spreekt niemand hierover. Historici kennen de formule immers niet toe aan hem, maar aan de Schot James Gregory, die ze pas in 1667 officieel zou ‘ontdekken’. Madhava had ook gelijkaardige formules voor de sinus en de cosinus. Hij was de eerste die  reeksen gebruikte om goniometrische functies te benaderen. Deze formules zijn tot bij ons beland via de jezuïten.