Tag archieven: gelijkzijdige driehoek

Stelling van Viviani

Geplaatst op door

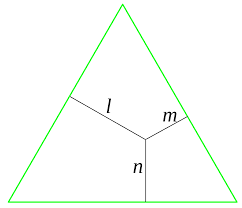
Kies een punt binnen een gelijkzijdige driehoek. Bereken de afstand van dit punt tot de drie zijden van de driehoek. Waar je dit punt ook plaatst de som van die afstanden is gelijk aan de hoogte van de driehoek.

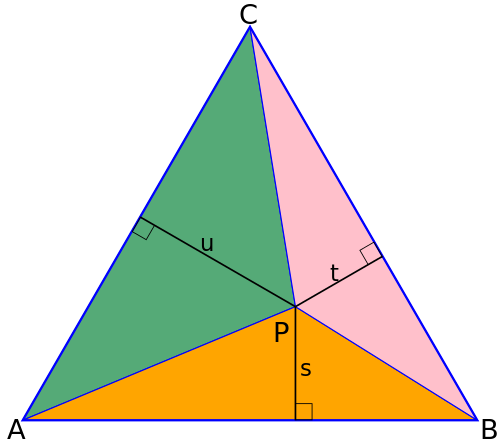
De stelling kan eenvoudig bewezen worden. Noem het punt P en de driehoek ABC. De oppervlakte van ABC is gelijk aan de som van de oppervlakten van de driehoeken PAB, PAC en PBC. Hieruit volgt het gestelde.

Deze stelling is vernoemd naar de Italiaanse wiskundige en wetenschapper Vincenzo Viviani( 1622-1703).

We kunnen de eigenschap ook veralgemenen tot een regelmatige n-hoek. In dat geval is de som van de afstanden vanuit een punt binnen de veelhoek naar de n zijden gelijk aan n keer het apothema van de veelhoek.Zelfs het omgekeerde is waar: wanneer de som van de minimale afstanden naar elk van de zijden van een veelhoek onafhankelijk is van het gekozen punt binnen de veelhoek, dan is het een regelmatige veelhoek .

Een eigenschap van gelijkzijdige driehoeken.

Geplaatst op door

Gegeven zijn 2 punten A en B. Als we B roteren  over 60° rond A, naar het punt B’, dan is de driehoek ABB’ gelijkzijdig.

Een gevolg hiervan is de volgende eigenschap over gelijkzijdige driehoeken die gevonden werd in 1936 door de Roemeense wiskundige D.Pompeiu (1873-1954). Het is merkwaardig dat dit, relatief eenvoudig resultaat, niet vroeger ontdekt werd.

ABC is een gelijkzijdige driehoek en P een punt dat niet op de omgeschreven cirkel ligt van ABC. Dan is het steeds mogelijk een driehoek te construeren met als zijden PA,PB en PC. Als P toch op de omgeschreven cirkel ligt dan zal een van deze drie lengtes gelijk zijn aan de som van de anderen.

In onderstaande tekening wordt ABC over 60° gedraaid rond het punt C. De zijden van de driehoek PP’A zijn gelijk aan PA,PB en PC, dus hebben we inderdaad een driehoek geconstrueerd met als zijden PA,PB en PC.