Ravi substitutie | Wiskunde is leuk

De Ravi substitutie is een techniek die erg belangrijk is bij het oplossen van meetkundige ongelijkheden. Ze luidt als volgt:

Als a, b en c zijden van een driehoek zijn dan bestaan er positieve getallen x,y en z zodat

$a = y + z, b = z + x \text{ en } z = x + y$

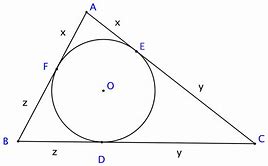
Het bewijs hiervan is niet zo lastig. Als a ,b en c zijden zijn van een driehoek, dan kunnen we de ingeschreven cirkel tekenen en uit onderstaande tekening volgt het gestelde.

Omgekeerd, zijn a, b en c de zijden van een driehoek als elke zijde kleiner is dan de som van de twee andere zijden. En dat is evident omdat x,y en z positief zijn.

Voorbeeld: Als a, b en c de zijden van een driehoek zijn bewijs dan dat

$abc \geq (b+c-a)(c+a-b)(a+b-c)$

We gebruiken de Ravi substitutie en we moeten dan bewijzen dat :

$(y+z)(z+x)(x+y)\geq xyz$

$x(y-z)^2+y(z-x)^2+z(x-y)^2\geq 0$

Omdat x,y en z positief zijn is dit correct.

De naam Ravi substitutie komt van de Canadese wiskundige Ravi D. Vakil, (geboren in 1970) die deze reeds gekende substitutie als één van zijn favoriete methodes gebruikte bij het oplossen van ongelijkheden. Hij was lid van het Canadese team bij de Internationale Wiskunde Olympiade in 1986,1987 en 1988 en behaalde zilver en twee maal goud (éénmaal met een perfecte score).