Tag archieven: ongelijkheden

Nootje 23

Geplaatst op door

Bereken de oppervlakte van het gebied bepaald door

    \[|x|+|y|+|x+y|\leq 1\]

Antwoord

 

 

  • In het eerste kwadraat is x>0 en y>0 en dus ook x+y>0. De gegeven ongelijkheid wordt dan x+y\leq \frac{1}{2}.
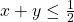  • In het derde kwadrant is x<0 en y<0 en dus ook x+y<0. De ongelijkheid wordt dan x+y\geq -\frac{1}{2}.
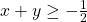  • In het tweede kwadrant is x<0 en y>0. Als x+y>0 wordt de ongelijkheid 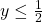 y\leq \frac{1}{2}. Is echter x+y<0, dan verkrijgen we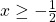 x\geq -\frac{1}{2}
  • In het vierde kwadrant tenslotte is x>0 en y<0. Als x+y>0, dan is de ongelijkheid 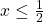x\leq \frac{1}{2}. Is daarentegen x+y<0, dan krijgen we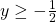 y\geq - \frac{1}{2}
  • Het stelsel van al die ongelijkheden geeft volgend gebied in het vlak:
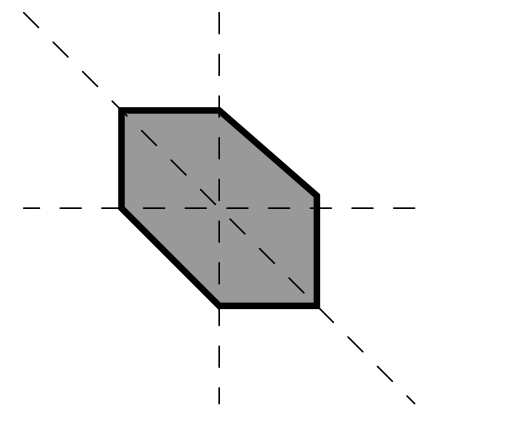
  • In deze figuur herkennen we gemakkelijk drie vierkanten met zijde 1. De oppervlakte is dus 3 oppervlakte eenheden

 

Majorisatie ongelijkheid

Geplaatst op door

Neem 2 geordende n-tallen x_1,\cots,x_n en y_1,\cdots,y_n. Als x_1 \geq x_2\geq \cdots \geq x_n,
y_1\geq y_2\geq \cdots \geq y_n,
x_1\geq y_1,
x_1+x_2\geq y_1+y_2, …,
x_1+x_2+\cdots+x_{n-1}\geq y_1+y_2+\cdots+y_{n-1} en x_1+\cdots+x_n=y_1+\cdots+y_n, dan zeggen we dat het n-tal (x_1,\cdots,x_n) het n-tal (y_1,\cdots,y_n) majorizeert en we noteren (x_1,\cdots,x_n)>(y_1,\cdots,y_n).

Dit gaan we gebruiken in volgende stelling over ongelijkheden:

Als f een convexe functie is op een interval I en (x_1,\cdots,x_n)>(y_1,\cdots,y_n) met x_i,y_i \in I, dan zal

    \[f(x_1)+\cdots+f(x_n)\geq f(y_1)+\cdots+f(y_n)\]

  • Als f strikt convex is krijg je een gelijkheid als en slechts als \forall i: x_i=y_i.
  • Er is een gelijkaardig resultaat voor concave functies, als je de ongelijkheidstekens omdraait.
  • Deze stelling is een veralgemening van de ongelijkheid van Jensen, waarbij (x_1,\cdots,x_n)> (x,\cdots,x). Hierbij is x het rekenkundig gemiddelde van de getallen x_i.

Een voorbeeld:

Vind de maximum waarde van a^{12}+b^{12}+c^{12} als -1\leq a,b,c \leq 1 en a+b+c=-\frac{1}{2}.

  • De functie f(x)=x^{12} is convex op \left[-1,1\right], want f''(x)=132x^{10}\geq 0 op \left[-1,1\right].
  • Veronderstel 1\geq a \geq b\geq c\geq -1.
  • Dan is (1,-\frac{1}{2},-1)>(a,b,c), want eerst en vooral is 1\geq a. Verder is -c\leq 1, dus is 1-\frac{1}{2} \geq -c-\frac{1}{2}=a+b.
  • Volgens de majorisatie ongelijkheid is dan a^{12}+b^{12}+c^{12} \leq f(1)+f(-\frac{1}{2})+f(-1)=2+\frac{1}{2^{12}}.
  • De maximumwaarde van 2+\frac{1}{2^{12}} wordt bereikt voor a=1, b=-\frac{1}{2} en c=-1.

Goniometrische substituties

Geplaatst op door

We kennen het gebruik van een goniometrische substitutie bij het berekenen van onbepaalde integralen. Maar ze kunnen ook hun nut hebben bij de studie van ongelijkheden. Een voorbeeld:

Als a,b,c,en d positieve reële getallen zijn en

    \[\frac{1}{1+a^4}+\frac{1}{1+b^4}+\frac{1}{1+c^4}+\frac{1}{1+d^4}=1\]

bewijs dan dat abcd \geq 3.

  • Stel a^2=\tan x, b^2=\tan y,c^2=\tan z en d^2=\tan t
  • Omdat 1+\tan^2x=\frac{1}{\cos^2x} wordt de gegeven ongelijkheid: \cos^2x+\cos^2y+\cos^2z+\cos^2t=1
  • We gebruiken nu de ongelijkheid van het rekenkundig en meetkundig gemiddelde: \sin^2x=1-\cos^2x=\cos^2y\cos^2z\cos^2t \geq 3(\cos y.\cos z.\cos t)^{\frac{2}{3}}
  • Analoog \sin^2y\geq 3(\cos x.\cos z.\cos t)^{\frac{2}{3}}.
  • Of \sin^2z\geq 3(\cos x.\cos y.\cos t)^{\frac{2}{3}}.
  • En \sin^2t\geq 3(\cos x.\cos y.\cos z)^{\frac{2}{3}}.
  • Als we nu deze 4 ongelijkheden met elkaar vermenigvuldigen vinden we dat \sin^2x.\sin^2y.\sin^2z.\sin^2t \geq 81 \cos^2x.\cos^2y.\cos^2z.\cos^2t.
  • Hieruit volgt dat \tan^2x.\tan^2y.\tan^2z.\tan^2t \geq 81 of a^4b^4c^4d^4 \geq 81.
  • Omdat a,b,c en d positief zijn volgt hieruit dat abcd \geq 3.

Ongelijkheid van Erdös-Mordell

Geplaatst op door

Deze ongelijkheid vertelt ons dat, voor een punt in het inwendige van een driehoek, dat de som van de afstanden tot de hoekpunten niet kleiner is dan het dubbel van de som van de afstanden tot de zijden van de driehoek. Dit werd door Paul Erdös( 1913-1996) als een vermoeden geformuleerd in 1935 en in hetzelfde jaar nog bewezen door de Britse wiskundige Louis Mordell (1888-1972).

    \[x+y+z \geq 2(a+b+c)\]

  • b+y\geq h_B, dus is \frac{1}{2}|AC|(b+y)\geq\frac{1}{2}(|AC|b+|BC|a+|AB|c). Hieruit volgt dat |AC|y\geq |BC|a+|AB|c.
  • Door het inwendig punt te spiegelen rond de bissectrice van C, vinden we dat |AC|y\geq |BC|c+|AB|a.
  • Analoge redeneringen geeft ook dat |AB|z\geq |BC|b+|AC|a en |BC|x\geq |AC|c+|AB|b.
  • Oplossen naar x,y en z geeft dit x\geq \frac{|AC|}{|BC|}c+\frac{|AB|}{|BC|}b,  y\geq \frac{|BC|}{|AC|}c+\frac{|AB|}{|AC|}a, en z\geq \frac{|BC|}{|AB|}b+\frac{|AC|}{|AB|}a.
  • Lid per lid  optellen van deze ongelijkheden geeft: x+y+z \geq ( \frac{|AC|}{|BC|}+ \frac{|BC|}{|AC|})c+( \frac{|BC|}{|AB|}+ \frac{|AB|}{|BC|})c+( \frac{|AC|}{|AB|}+ \frac{|AB|}{|AC|})b.
  • Uit de ongelijkheid over het rekenkundig en meetkundig gemiddelde volgt dat de coëfficiënten van a,b en c alle groter of gelijk zijn aan 2, zodat x+y+x \geq 2(a+b+c).

Ravi substitutie

Geplaatst op door

De Ravi substitutie is een techniek die erg belangrijk is bij het oplossen van meetkundige ongelijkheden. Ze luidt als volgt:

Als a, b en c zijden van een driehoek zijn dan bestaan er positieve getallen x,y en z zodat 

    \[a = y + z, b = z + x \text{ en } z = x + y\]

Het bewijs hiervan is niet zo lastig. Als a ,b en c zijden zijn van een driehoek, dan kunnen we de ingeschreven cirkel tekenen en uit onderstaande tekening volgt het gestelde.

Omgekeerd, zijn a, b en c de zijden van een driehoek als elke zijde kleiner is dan de som van de twee andere zijden. En dat is evident omdat x,y en z positief zijn.

Voorbeeld: Als a, b en c de zijden van een driehoek zijn bewijs dan dat

    \[abc \geq (b+c-a)(c+a-b)(a+b-c)\]

We gebruiken de Ravi substitutie en we moeten dan bewijzen dat :

    \[(y+z)(z+x)(x+y)\geq xyz\]

  of

    \[x(y-z)^2+y(z-x)^2+z(x-y)^2\geq 0\]

Omdat x,y en z positief zijn is dit correct.

De naam Ravi substitutie komt van de Canadese wiskundige Ravi D. Vakil, (geboren in 1970) die deze reeds gekende substitutie als één van zijn favoriete methodes gebruikte bij het oplossen van ongelijkheden. Hij was lid van het Canadese team bij de Internationale Wiskunde Olympiade in 1986,1987 en 1988 en behaalde zilver en twee maal goud (éénmaal met een perfecte score).