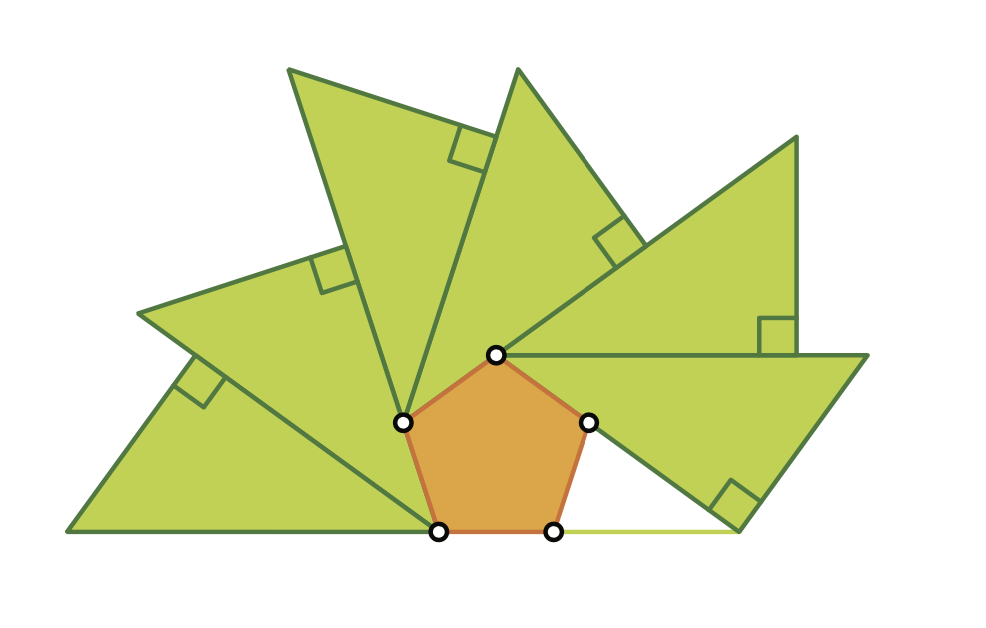
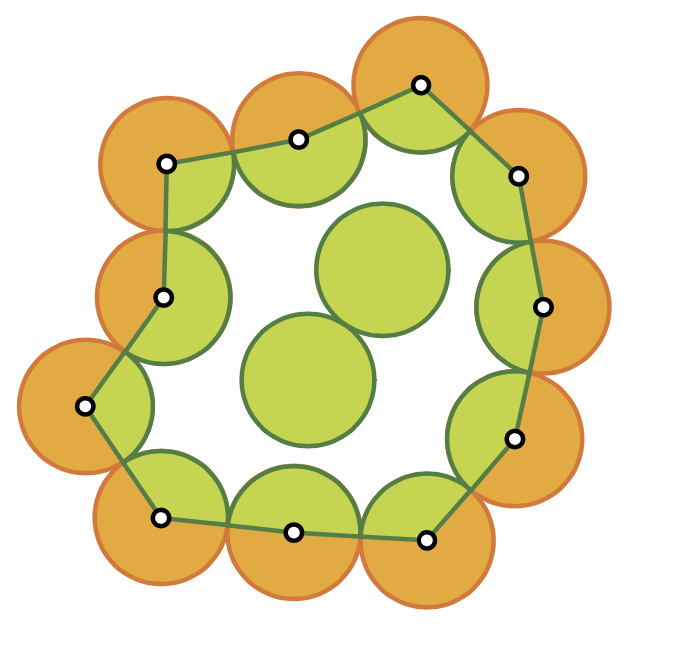
Deze sangaku werd beschreven op een tablet van de Miyagi Prefecture uit 1912
Antwoord
- We gaan op zoek naar de lengte van de schuine zijde van de groene rechthoekige driehoeken. Noteer de zijde van de regelmatige vijfhoek door a.
- We leggen volgende notatie vast:

- De scherpe hoek van de groene driehoek, die grenst aan de vijfhoek is
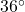 (de helft van het supplement van de hoek van een vijfhoek, en die is
(de helft van het supplement van de hoek van een vijfhoek, en die is 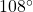 ).
). - Driehoek
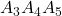 is gelijkbenig en dus zijn de basishoeken elk
is gelijkbenig en dus zijn de basishoeken elk 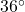 . Volgens de cosinusregel is
. Volgens de cosinusregel is 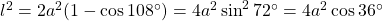
- Hieruit volgt dat
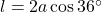 .
. - In driehoek
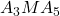 is
is 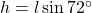 . Samen met vorig resultaat geeft dit dat
. Samen met vorig resultaat geeft dit dat 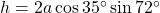 .
. - In driehoek
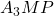 is
is 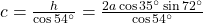 .
. - Tenslotte, in driehoek
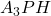 is
is 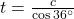 .
. - Hierin kunnen we c invullen en krijgen we, omdat
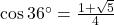 :
: ![Rendered by QuickLaTeX.com \[t=a(1+\sqrt{5})\]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-b35c5b80a6d5e60ab67b4d0ed1f5340b_l3.png)