Tag archieven: spiegelingen

Een meetkundige parel

Geplaatst op door

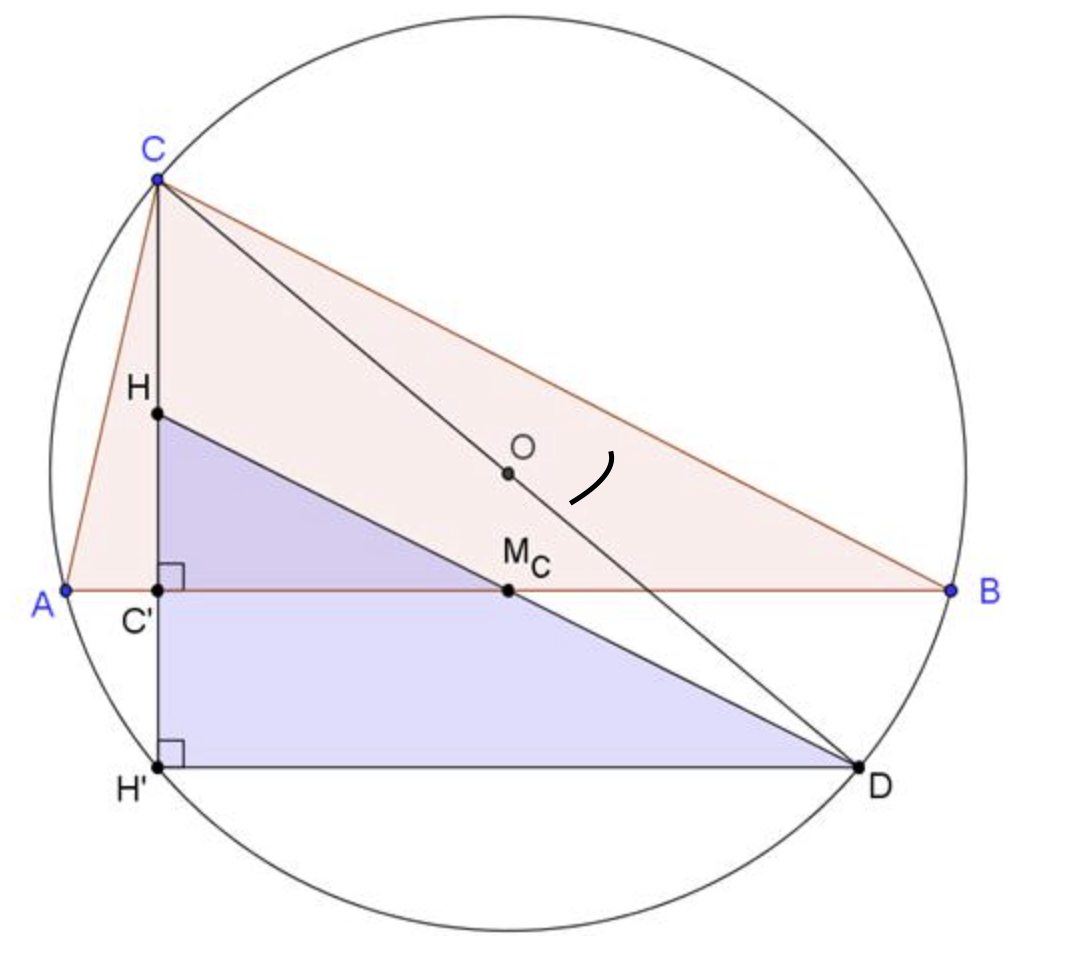
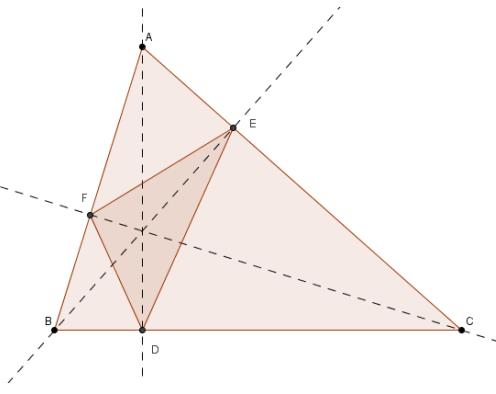
Onlangs vond ik volgende stelling die ik helemaal niet kende. Een echt pareltje: De spiegelbeelden van het hoogtepunt van een driehoek ABC rond de zijden en rond de middens van de zijden liggen op de omgeschreven cirkel van ABC.

H’ is het spiegelbeeld van H (hoogtepunt) rond de zijde AB en CD is een middellijn van de omgeschreven cirkel.

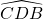  • \widehat{CDB} is een rechte hoek, als omtrekshoek op een halve cirkel. Omdat AH loodrecht op BC staat, zijn BD en AH evenwijdig.
  • Analoog is AD ook evenwijdig met BH.
  • Dus is AHBD een parallellogram. 
  • Omdat de diagonalen van een parallellogram elkaar midden doordelen is 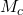M_c het midden van AB en dus is D inderdaad het spiegelbeeld van H bij een puntspiegeling rond het midden van B.
  • Omdat HC’=C’H’ is 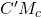C'M_c de middenparallel van driehoek HH’D en staat DH’ loodrecht op CC’ omdat DH’ evenwijdig is met C'M_c.
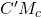  • Dus is 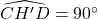\widehat{CH'D}=90^\circ  en wegens de eigenschappen van omtrekshoeken ligt dus H’ op de omgeschreven cirkel van driehoek ABC.

Het probleem van Fagnano

Geplaatst op door

Gegeven is een scherphoekige driehoek ABC. Zoek een ingeschreven driehoek DEF  met de kleinst mogelijke omtrek.

Dit probleem werd in 1775 gesteld door de Italiaanse wiskundige J.F.Fagnano.

Eén van heuristieken gebruikt bij problem solving leert ons het probleem aan te pakken voor een speciaal geval: neem het  punt D  vast. Spiegel vervolgens D rond de twee aanliggende zijden tot S en T. 

De omtrek van DEF is gelijk aan de lengte van SFET. De kleinst mogelijke omtrek krijgen we dus als als SFET zo klein mogelijk is, dus als we F en E nemen op de rechte ST.
Merk op dat de driehoek SAT gelijkbenig is en dat de tophoek SAT gelijk is aan het dubbele van de hoek BAC. Aangezien het lijnstuk [ST] de basis is van een gelijkbenige driehoek met een vaste tophoek, zal deze basis zo klein mogelijk zijn als de lengte van de benen [AS] en [AT] zo klein
mogelijk is. We moeten het punt D dus zo kiezen dat [AS] en [AT] zo klein mogelijk zijn. Het is duidelijk dat |AS| = |AD| = |AT|. We moeten dus D op [BC] kiezen zodat|AD| zo klein mogelijk is. Bijgevolg moet D het voetpunt zijn van de loodlijn uit A op [BC] . 

Natuurlijk kunnen we in plaats van met D te beginnen ook via E of F werken. Zo krijgen we als oplossing de voetpuntsdriehoek:

 

 

Constructies in verband met ontoegankelijkheid

Geplaatst op door

We bestuderen constructies  die we normaal gesproken wel kunnen uitvoeren, maar die nu niet uit te voeren zijn omdat bepaalde delen van de figuur ontoegankelijk zijn. Om zulke constructies uit te voeren zijn spiegelingen rond een as uitermate geschikt. We weten immers dat een spiegeling evenwijdigheid, loodrechtheid en ook afstanden en hoeken bewaart. Hierdoor wordt het mogelijk bepaalde gegevens toch bereikbaar te maken.



Bepaal de bissectrice van de twee gegeven rechten.}




    

  •  Teken een willekeurige rechte m die de twee gegeven rechten (die we a en b noemen) snijdt.
    • 

  • Spiegel de gegeven rechten rond m: a' en b'.
    • 

  • Bepaal het snijpunt S van a' en b'.
    • 

  • Construeer de bissectrice d van a' en b'. Dit is een basisconstructie.
    • 

  • Bepaal tenslotte het spiegelbeeld d', bij spiegeling van d rond m.
    •