Wiskunde is leuk

Opgave 28

Geplaatst op 22 april 2019 door admin

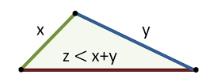
Hoeveel niet-congruente driehoeken met gehele zijden en omtrek 2019 kan men construeren?

Antwoord

Elke zijde van een driehoek is kleiner dan de som van de twee andere zijden. Bijgevolg is de langste zijde van de gezochte driehoeken $\leq 1009$ .
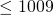Stel dat de langste zijde gelijk is aan 1009, dan kunnen de andere twee zijden gelijk zijn aan : 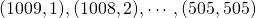$(1009,1),(1008,2),\cdots,(505,505)$ . Er zijn dus 505 mogelijke driehoeken.
Stel dat de langste zijde gelijk is aan 1008, dan kunnen de andere zijden gelijk zijn aan: 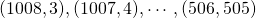$(1008,3),(1007,4),\cdots,(506,505)$ . Er zijn dus 503 mogelijke driehoeken.
Stel dat de langste zijde gelijk is aan 1007, dan kunnen de andere zijden gelijk zijn aan: 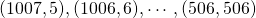$(1007,5),(1006,6),\cdots,(506,506)$ . Er zijn dus 502 mogelijke driehoeken.
Daal verder af…
Stel dat de langste zijde gelijk is aan 674, dan kunnen de andere zijden gelijk zijn aan: 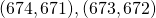$(674,671),(673,672)$ . Er zijn dus 2 mogelijke driehoeken.
Tenslotte blijft er de gelijkzijdige driehoek met zijde 673 over.
Het totaal aantal mogelijkheden is $S=505+503+502+500+\cdots+4+2+1$ .
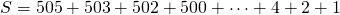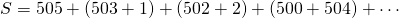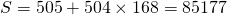Herschikking geeft $S=505+(503+1)+(502+2)+(500+504)+\cdots$ . Dit geeft $S=505+504 \times 168 =85177$ .

Opgave 8

Geplaatst op 18 december 2017 door admin

Als a,b en c de maatgetallen voorstellen van de zijden van een driehoek, dan geldt

$\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}<2$

Antwoord

Omdat a,b en c de maatgetallen voorstellen van de zijden van een driehoek, weten we dat elke zijde kleiner is dan de som van de twee andere zijden. Dus bijvoorbeeld $a<b+c$
Dan is $\frac{a}{b+c}=\frac{2a}{2(b+c)}=\frac{2a}{(b+c)+(b+c)}$ .
Door toepassing van de driehoeksongelijkheid op het eerste deel van de noemer vinden we dat
$\frac{a}{b+c}<\frac{2a}{a+b+c}$

.
Op analoge wijze vinden we dat $\frac{b}{c+a}<\frac{2b}{a+b+c}$ en $\frac{c}{a+b}<\frac{2c}{a+b+c}$ .
Alles samenvoegen geeft
$\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}< \frac{2a+2b+2c}{a+b+c}=2$

Driehoeken

Geplaatst op 8 april 2017 door admin

Bekijken we enkele eigenschappen over zijden en hoeken in een willekeurige driehoek:

De som van de hoeken van een driehoek is 180°
Een buitenhoek van een driehoek is groter dan elke niet aanliggende binnenhoek ( $\delta > \alpha$ en $\delta > \beta$ )
In een driehoek ligt, tegenover een grotere zijde, een grotere hoek en omgekeerd tegenover een grotere hoek ligt een grotere zijde.
Elke zijde van een driehoek is kleiner dan de som van beide andere zijden. Je kan deze eigenschap veralgemenen naar veelhoeken: elke zijde van een veelhoek is kleiner dan de som van de andere zijden.