Bewijs dat geen enkel getal van de vorm
![]()
- Veronderstel dat er toch een natuurlijk getal k bestaat zodat
![Rendered by QuickLaTeX.com \[3^3+3^n+2=k^2\]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-160bc1368dc28270a885e291c1cb179a_l3.png)
- Dan is
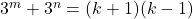 . Omdat het linkerlid even is en omdat
. Omdat het linkerlid even is en omdat 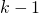 en
en  dezelfde pariteit hebben, zijn
dezelfde pariteit hebben, zijn 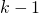 en
en  opeenvolgende even getallen.
opeenvolgende even getallen. - Dit betekent ook dat ofwel
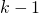 ofwel
ofwel  een viervoud is. Het rechterlid
een viervoud is. Het rechterlid 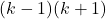 is dus deelbaar door 8.
is dus deelbaar door 8. - Bij deling door 8 zijn de resten van machten van 3 ofwel 1 ofwel 3. De som
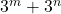 is dus modulo 8, gelijk aan 2,4 of 6 en dus zeker niet deelbaar door 8.
is dus modulo 8, gelijk aan 2,4 of 6 en dus zeker niet deelbaar door 8. - Bijgevolg kan
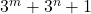 nooit een volkomen kwadraat zijn.
nooit een volkomen kwadraat zijn.



