Er liggen 50 jetons op een rij. Op elke jeton staat een natuurlijk getal en de som van al die getallen is oneven. Joeke en Nienke nemen om beurten een jeton weg die aan één van de uiteinden van de rij ligt. Joeke mag beginnen. We tellen de getallen van de genomen jetons bij elkaar op. Bewijs dat Joeke een strategie kan bedenken waarbij zij, in het totaal, de grootste som heeft.
Antwoord
- We kleuren de jetons, alternatief, van links naar rechts, blauw of zwart.
- Joeke neemt een jeton. Wanneer ze terug aan de beurt is, zal er zeker een jeton beschikbaar zijn in dezelfde kleur die ze in het begin genomen heeft.
- Dus kan ze er voor zorgen dat ze alle jetons van eenzelfde kleur neemt. Nienke heeft dan alle jetons van de andere kleur.
- Nu kunnen ze nooit dezelfde som hebben want dan zou de som van alle jetons even zijn.
- Dus ofwel neemt Joeke alle blauwe jetons ofwel alle zwarte.
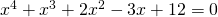 ?
?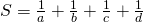 .
.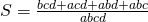
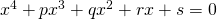 gelijk is aan s. Bijgevolg is
gelijk is aan s. Bijgevolg is 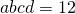 .
.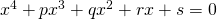 is -r. Bijgevolg is
is -r. Bijgevolg is 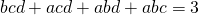 .
.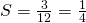 .
.