Tag archieven: kleine nootjes
Nootje 46
Bereken
![]()
Antwoord
- Een mogelijkheid is om het binomium van Newton te gebruiken. Gaan we niet doen…
- Stel
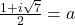 en
en 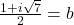 .
. - Dan is
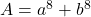 .
. - Nu is het duidelijk dat
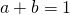 en
en 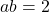 .
. - We weten dat
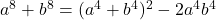 . Analoog is
. Analoog is 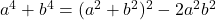 en evenzo is
en evenzo is 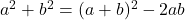 .
. - De laatste betrekking leert ons dat
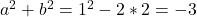 .
. - Dan is
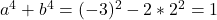 .
. - Tenslotte is
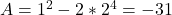 .
.
Nootje 45
Zoek een getal van 4 cijfers, waarbij elk cijfer kleiner is dan 7. Het getal is een kwadraat en als je bij elk cijfer 3 optelt bekom je opnieuw een getal dat een kwadraat is.
Antwoord
- Noteer met x het gezochte getal.
- Dan kan je schrijven dat
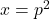 met p tussen 31 en 100.
met p tussen 31 en 100. - Elk cijfer mer 3 vermeerderen betekent dat je 3333 optelt bij x.
- Deze uitkomst is weer het kwadraat van een getal: Noteer dit als
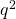 .
. - Dan is
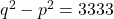 of
of 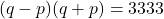 .
. - Nu kan je 3333 schrijven als
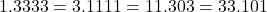 .
. - Zo bekom je bvb het stelsel
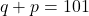 en
en 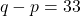 , waaruit volgt dat p=34
, waaruit volgt dat p=34 - De andere mogelijkheden leveren geen oplossing op voor p tussen 32 en 100.
- Het gezocht getal is dus
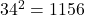
Nootje 42
Nootje 38
Antwoord
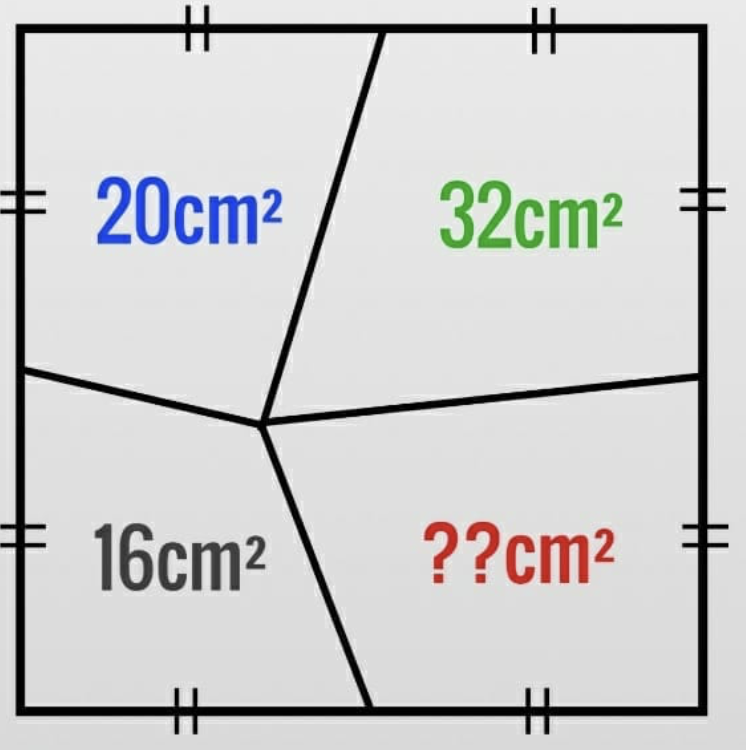
- Onderverdelen in driehoeken lijkt een goed idee:
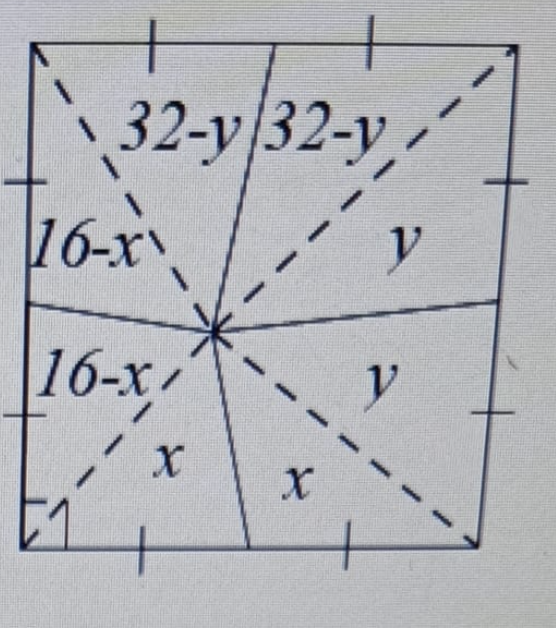
- De gelijkheid van oppervlaktes is evident: zelfde hoogte en even grote basis.
- De vierhoek linksboven heeft oppervlakte 20 en is dus gelijk aan
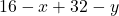 .
. - Hieruit volgt
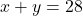 .
. - De oppervlakte van de vierhoek rechts onder, die gevraagd wordt, is gelijk aan
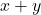 , dus de gevraagde oppervlakte is gelijk aan 28 vierkante centimeter.
, dus de gevraagde oppervlakte is gelijk aan 28 vierkante centimeter.