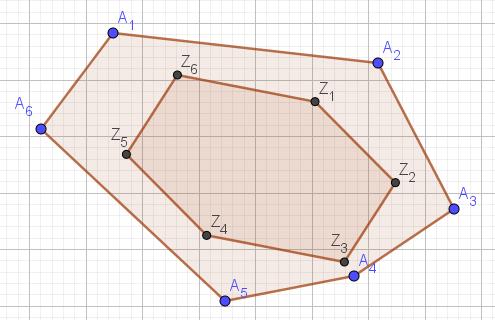
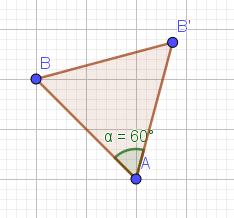
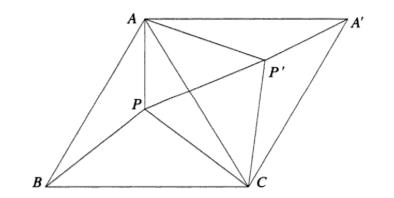
Neem een willekeurige convexe zeshoek. Met telkens drie opeenvolgende hoekpunten van deze zeshoek vormt men zes driehoeken. Construeer het zwaartepunt van deze driehoeken. De alzo verkregen punten zijn de hoekpunten van een nieuwe zeshoek. Toon aan dat de paren overstaande zijden van deze zeshoek evenwijdig en even lang zijn.
We geven de hoekpunten ![]() van de oorspronkelijke zeshoek willekeurige coördinaten
van de oorspronkelijke zeshoek willekeurige coördinaten ![]() ( drievouden omdat we het zwaartepunt moeten berekenen). Het zwaartepunt van driehoek
( drievouden omdat we het zwaartepunt moeten berekenen). Het zwaartepunt van driehoek ![]() is het punt
is het punt ![]() . Analoge coördinaten voor de andere hoekpunten. We proberen nu aan te tonen dat
. Analoge coördinaten voor de andere hoekpunten. We proberen nu aan te tonen dat ![]() evenwijdig is met
evenwijdig is met ![]() en dat
en dat ![]() .
.
- De richtingsgetallen van
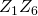 zijn
zijn 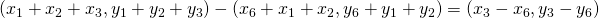 De richtingsgetallen van
De richtingsgetallen van 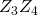 zijn
zijn 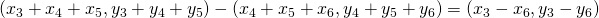 Bijgevolg is
Bijgevolg is 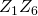 evenwijdig met
evenwijdig met 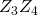 .
. 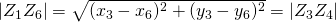 .
.