Deze bewijstechniek bestaat er in ‘een verhaaltje te vertellen.
Stel ik wil volgende formule “bewijzen”: voor ![]()
![]()
Je zou natuurlijk, gebruikmakend van de definitie van de binomiaalgetallen, beide leden kunnen uitrekenen, en vaststellen dat beide resultaten hetzelfde zijn. Maar proberen we dit eens anders in te kleden. Je hebt binnen een politieke partij n kaderleden, waaruit je een dagelijks bestuur van p personen moet kiezen, met hierin een voorzitter en een ondervoorzitter. Dit kan je doen op twee manieren :
- Kies eerst p personen. Dit kan op
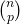 . Kies hier uit een voorzitter: p mogelijkheden. Kies dan een ondervoorzitter: p – 1 mogelijkheden. Samen geeft dit dus, als aantal mogelijkheden:
. Kies hier uit een voorzitter: p mogelijkheden. Kies dan een ondervoorzitter: p – 1 mogelijkheden. Samen geeft dit dus, als aantal mogelijkheden: ![Rendered by QuickLaTeX.com \[p(p-1)\binom{n}{p}\]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-91330e6fd38d763d52eeea2300774cae_l3.png)
- Maar je kan eerst een voorzitter kiezen uit de n kaderleden. Dit kan je op n mogelijkheden. Kies vervolgens een ondervoorzitter: n – 1 mogelijkheden. Kies tenslotte nog p-2 ander personen om je dagelijks bestuur te vervolledigen. dit kan op
 manieren. Zo krijg je in het totaal als mogelijkheden:
manieren. Zo krijg je in het totaal als mogelijkheden: ![Rendered by QuickLaTeX.com \[n(n-1)\binom{n-2}{p-2}\]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-aa85089223ed202eb9d7fc2c111cd64e_l3.png)
Hiermee is de gevraagde formule bewezen!




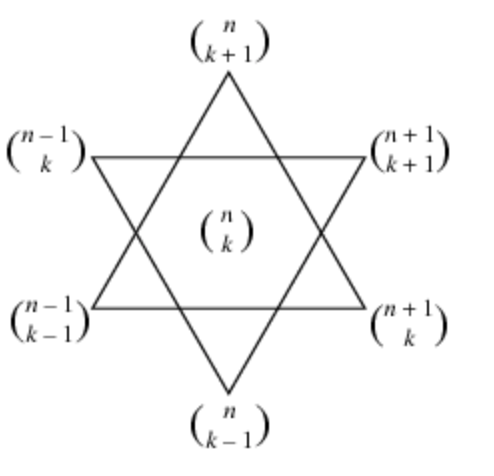
![Rendered by QuickLaTeX.com \[n=\sum_{i=0}^hn_i.2^{h-i}\]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-0a461b163b130555b12f5672bfe5a547_l3.png)
![Rendered by QuickLaTeX.com \[s=\sum_i^ps_i.2^{p-i}\]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-ba1bb5df96b961585aeab0256809b2c5_l3.png)