Tag archieven: Bewijstechnieken

Maak een tekening

Geplaatst op door

Soms kan het een grote hulp zijn de gegevens van het probleem te visualiseren. We denken dan uiteraard aan een meetkundig probleem waar een tekening ons kan helpen tot een oplossing te komen. Maar je kan ook werken met een Venndiagram, een boomschema of met grafen om je gedachten te ordenen.

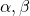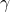Neem een driehoek ABC met hoeken \alpha,\beta en \gamma. Bewijs dan:

    \[\dfrac{\sin \alpha+\sin \beta}{2}\leq \sin \dfrac{\alpha+\beta}{2}\]

  • Je kan proberen de ongelijkheid te bewijzen via een tekenschema. Nuttig hierbij zullen waarschijnlijk de formules van Simpson zijn.
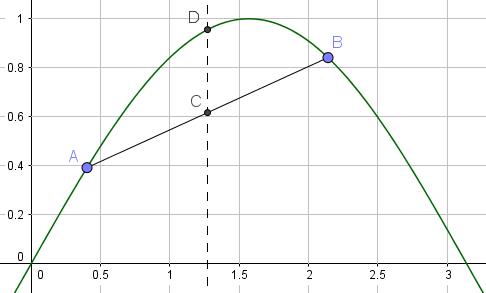
  • Maar bekijken we eens de grafiek van de sinusfunctie. Veronderstel 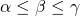\alpha \leq \beta \leq \gamma. De hoeken zijn uiteraard allen kleiner dan 180^\circ.
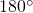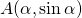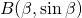  • A(\alpha,\sin \alpha) en B(\beta,\sin \beta). C is het midden van het lijnstuk [A,B].
  • Het linkerlid van de gegeven ongelijkheid is de hoogte van het punt C en het rechterlid de hoogte van het punt D. Door de bolle vorm van de grafiek van de sinusoïde in [0,\pi] is de ongelijkheid duidelijk. 
    

    • 



 



					

		
		
	


				
					
	

		

						
Kleuringen

			
						

				Geplaatst op   door  			

			
					


				

			
Soms kan het nuttig zijn om een rooster in te  kleuren  en daardoor te bewijzen dat een bepaalde situatie al dan niet mogelijk is. Deze heuristiek wordt dikwijls gebruikt wanneer je een schaakbord moet opvullen met bepaalde vormen.


Voorbeeld: Kan een 10 x 10 schaakbord opgevuld worden met 25 tetrominos van de vorm 


Oplossing:


    

  • Geef elk vakje van het schaakbord een uniek adres door het rijnummer en kolomnummer van het vakje te noteren. Zo een adres is dan van de vorm (i,j) \text{ waarbij } 1 \leq i,j \leq 10.
    • 

  • Kleur (i , j ) met de kleur t = i +j \text{ mod4 } zodat t \in \{1,2,3,4\}. Hierbij is1 = blauw; 2 = geel; 3 = rood; 4 = groen.
    

    • 

  • Elke tetromino zal door de schikking van de kleuren (cijfers) precies 4 vakjes met vier verschillende kleuren bedekken.
    • 

  • Aangezien er op het bord 25 keer blauw (1), 26 keer geel (2) 25 keer rood (3) en 24 keer groen (4) voorkomt zal het niet mogelijk zijn om het bord te vullen met 25 tetromino’s
    • 




					

		
		
	


				
					
	

		

						
Bewijstechnieken

			
						

				Geplaatst op   door  			

			
					


				

			
De geschiedenis van ’Bewijs dat …’ begint, net als een sprookje, vele,

vele jaren geleden met ’Er was eens…’. Er was inderdaad eens een tijd

waarin geen bewijzen bestonden nl, tijdens de Babylonische periode,

want in de Babylonische wiskunde – 4000 jaar geleden – was er geen

spoor te vinden van het begrip bewijs, noch van enige deductieve redenering.

Babylonische wiskunde, zoals ook deze tijdens de Egyptische farao’s,

bestond uit recepten om een concreet probleem met concrete gegevens

op te lossen. Het was een wiskunde zonder bewijzen, zonder verklaringen!

Toch bleek na verloop van tijd ergens de noodzaak voor meer

structuur omdat elk gelijkaardig probleem telkens moest worden hernomen

volgens het gegeven recept.


Lees hier over de verschillende bewijstechnieken.

bewijzen